Bayesian analysis is a powerful mathematical tool that uses certain relationships from probability theory. In MMI systems, it allows a number of mental efforts from one or more users to be combined to achieve higher accuracy for difficult tasks. An example of a difficult task is predicting future events that cannot be computed from existing information, such as the numbers that will be drawn in an upcoming lottery. For simplicity I will show how to use “Bayes’ Updating” to combine multiple MMI trials to provide a single bit of information with a calculated probability of being correct.
As background, there are three types of probabilities used in Bayesian analysis. The following are their brief definitions and more commonly used notations:
- Joint probability is the probability of both A and B occurring.It has a number of notations.
P(A ∩ B) = P(A and B) = P(A & B) = P(A, B) = P(A ^ B) - Conditional probability is the probability A occurs given B occurs or is assumed to occur.
P(A | B) = PB(A) - Marginal probability is the total probability of observing B independent of other events. The sum of all marginal probabilities must = 1.0.
P(B)
In addition, a number of variable names will be defined and used in the solution presented.
- Likelihood is the average probability that a measurement (a single mental effort or trial) will result in the correct answer. This is the hit rate (HR) of MMI trials. Note, the hit rate will vary both with the user and the specific type of task. Likelihood is measured and updated from real-world results. HR is always expected to be ≥ 0.5: psi missing or HR < 0.5 is not considered to be valid or useful.
- Prior is the presently believed probability that a specific state or answer is the correct one. The initial prior is defaulted to be 0.5, assuming there is no information to indicate otherwise.
- Posterior is the believed probability updated by an MMI trial (an observation or obs) that the specific state or answer is the correct one. After the posterior is calculated, its value is used as the prior for the next update.
- An observation, obs, is the result of an MMI trial. Obs can be either a 1 or a 0, but these symbols will typically represent an event, such as an increase or a decrease of a variable being predicted. A 1 or 0 symbol should always represent a meaning most closely associated with the symbol. A 1 will mean: up, higher, larger, stronger, faster, more, etc. A 0 will mean: down, lower, smaller, weaker, slower, less, etc. There are events or variables that have no clear or obvious association. In that case the best logical guess is used. Associate 1 with outer, even, white and hot. 0 would be associated with inner, odd, black, cold, etc. The user will learn by practice to connect the symbols with the variables. Always use the same associations.
For simplicity, the derivation of the Bayes’ updating for MMI use will not be presented here. The following algorithm and the definitions given above will allow a practical system to be implemented.
First, initialize the variables:
likelihood = hit rate determined by experience. If none is available, assume HR = 0.51;
prior = 0.5;
Calculate each posterior using a new MMI obs: Pass the three variables to the posterior function.
posterior (likelihood, prior, obs) = If (obs = 1) then,
posterior = (likelihood *prior)/((likelihood * prior) + (1 - prior)*(1 - likelihood)),
else,
posterior = ((1 - likelihood) * prior)/(prior * (1 - likelihood) + (1 - prior)*likelihood)
Return posterior.
set prior = posterior to be used as input for the next update.
Notes: the function for calculating the posterior depends on whether the obs is 1 or 0 so a conditional is used to select the proper one. It is assumed the language used calculates multiplications at a higher priority than addition so explicit parentheses are not required around multiplied variables when they are chained with additions.
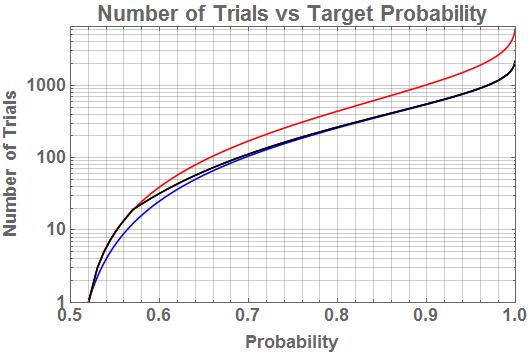
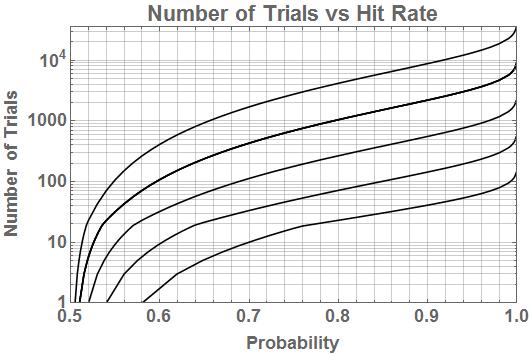
This algorithm calculates the posterior based on the assumption that the event represented by 1 is the correct one. If the posterior value returned is less than 0.5, that indicates a 0 is the true state and its probability is 1 – posterior. Generally, one wants to reach a high posterior value to have confidence it is correct and avoid false negative results. I suggest something around 0.95. This can take a large number of mental efforts, and the number is also highly variable. The number of efforts is strongly dependent on the actual HR of the user(s). When calculating a new posterior from multiple users, always use the likelihood achieved by the user who produced each obs. Entering a likelihood of 0.5 (pure chance) will not add any information nor change the posterior from the prior value.
Using incorrect likelihood values can have a number of undesirable results, though it will not prevent the algorithm from producing a result. If the likelihood is too low, a much larger number of trials can be required to reach a desired posterior value. If too high, fluctuations in posterior values will be exaggerated, causing more false negative results or reaching the threshold value too soon. If multiple users’ results are combined, misrepresenting their relative skill levels in the form of incorrect likelihoods can give too much or too little weight to their individual contributions.
Real-time user feedback is very important for best MMI results. When predicting a future event, it’s not possible to give feedback for that event since it has not yet been observed. Perhaps a trial-by-trial feedback can be given based on the size of a combined z-score or surprisal value (the ME Score for one trial). In addition, the running posterior value might be helpful, but it might also be misleading if the immediate value is in fact, incorrect, which can and will occur. Designing the best feedback will be a challenge.
One final note: in order to avoid conscious or unconscious bias, the polarity of the MMI data should be scrambled by randomly inverting blocks of data before they are combined to produce the final 1 or 0 output. The ME Trainer uses this approach for both the reveal and predict modes.